Introduction to Functions

For personal home schoolroom use only. Permission must be granted by the author for any other usage. Adapted from Paul A. Foerster’s Algebra and Trigonometry, section 4-4, pp. 126-133 (Pearson Prentice Hall, 2006).

Show the student two equations:

\(y = \frac{3}{4}x+3\)

\(y = \frac{5}{2}x-5\)

Ask the student to graph these two lines on a single Cartesian coordinate system. Here is an example of what the student would draw:

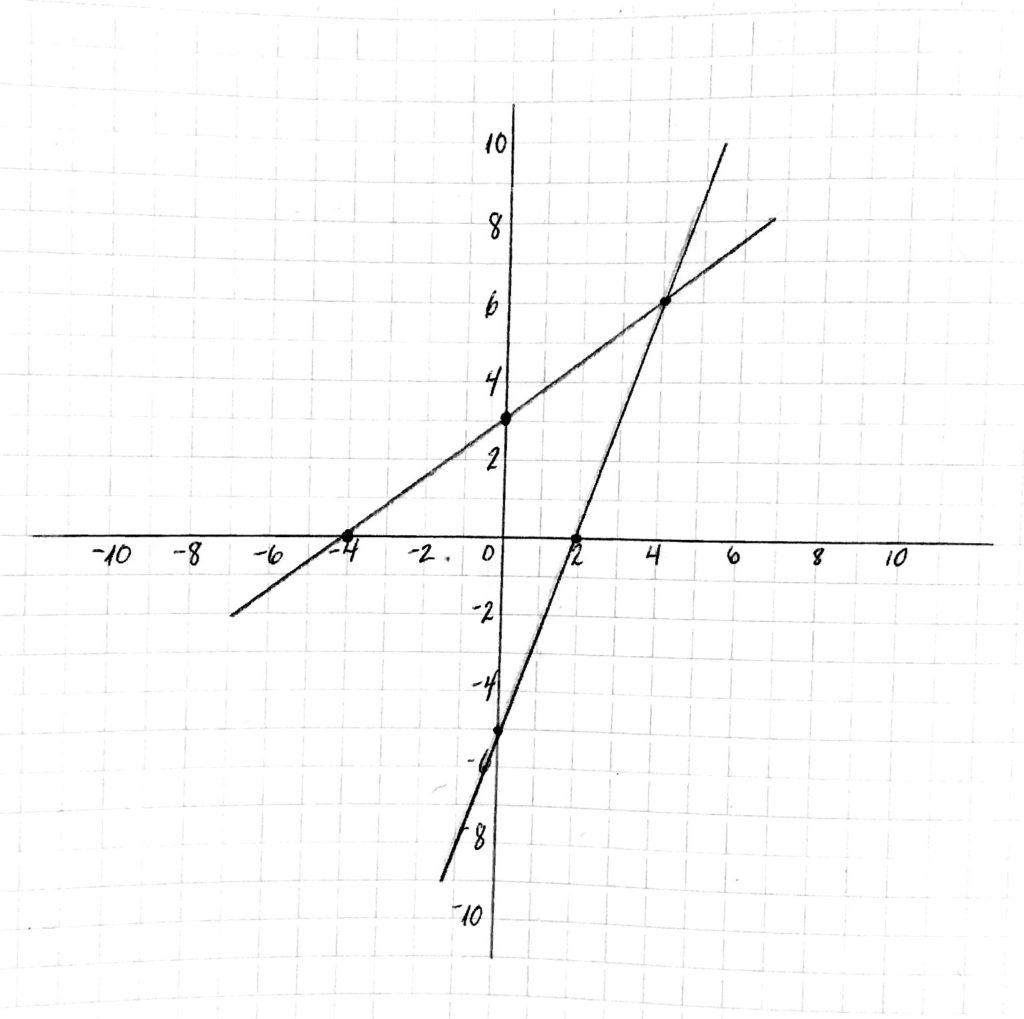
Ask: What observations can you make about these two lines?

What do they have in common? (possible answer: they have a positive slope)
How are they different? (possible answers: slope, intercepts)
Which is above the other?
Which is steeper?

What does y equal when x is 4? (help the student realize that this is an ambiguous question, since there are two lines)

How can we specify which y we want?
Do you have ideas how we could specify which line we are referring to?

What if we labeled the first one line f and the second one g?

Which equation has the steeper slope? (f or g?)
Which equation has a positive y-intercept? (f or g?)
What does y equal when x is 4, for f?
What does y equal when x is 4, for g?

Explain: Mathematicians use terminology and notation to differentiate between equations, or functions, with the same dependent variable. They write:

\(f(x) = \frac{3}{4}x+3\)

\(g(x) = \frac{5}{2}x-5\)

Instead of saying y equals 6 when x is 4, for f, they write:

\(f(4) = \frac{3}{4}\cdot4+3 = 3 + 3 = 6\)

And instead of saying y equals 5 when x is 4, for g, they write:

\(g(4) = \frac{5}{2}\cdot4-5 = 10 – 5 = 5\)

This notation was first used by Leonhard Euler in 1734, one of the most prolific mathemeticians in history.

f and g are called functions.

Can you think of any benefits of this function notation?

Let’s see what we can do with it. Here are two new function definitions:

\(f(x) = 3x + 11\)

\(g(x) = x^2 + x + 1\)

Evaluate together:

\(f(7)\)

\(g(-3)\)

\(\frac{f(5)}{g(5)}\)

\(f(g(2))\)

Evaluate alone:

\(f(0)\)

\(g(\frac{1}{3})\)

\(\frac{g(1)}{g(0)}\)

\(g(g(0))\)

Explain: One reason function notation is so powerful is that often functions have relationships between each other.

A large part of calculus involves relationships between functions.

This is especially true for calculus that applies to real world processes such as motion and acceleration.

Function notation give us a powerful and expressive way to explore these relationships, so that we can better understand dynamic processes in the real world.