A First Trigonometry Lesson
©2019 Art Middlekauff
For personal home schoolroom use only. Permission must be granted by the author for any other usage. Inspired by Paul A. Foerster’s Algebra and Trigonometry, chapter 13, pp. 711-718 (Pearson Prentice Hall, 2006).
Draw this figure on the white board:

Suppose a mouse walked from the center to the edge of the circle (the shaded line). How far will he have walked?
Encourage discussion here. The goal is for the student to say “1 radius.” If the student proposes a normal unit of measure, you can say something like this:
This mouse doesn’t really understand inches, feet, or meters. So let’s just say the mouse remembers the distance he walked and calls it “1 radius.”
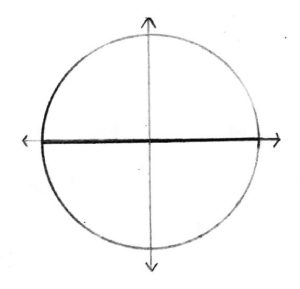 |
So our measuring stick is “1 radius.” If our mouse walked the whole diameter of the circle, how far will he have walked?
Answer: 2 radiuses |
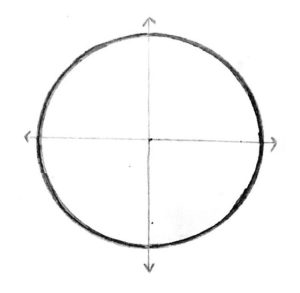 |
Suppose the mouse walked all the way around the circle. How many radiuses will he travel?
Answer: \(2\pi\) radiuses You may need to review the formula for the circumference of a circle: \(2\pi r\). In this case r is 1 radius, so the circumference is \(2\pi\) radiuses. |
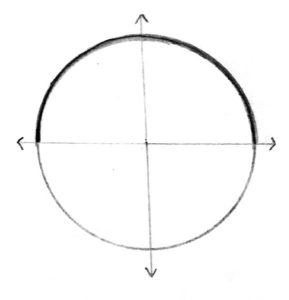 |
Suppose he only went halfway around the circle. How far will he have gone?
Answer: \(\pi\) radiuses |
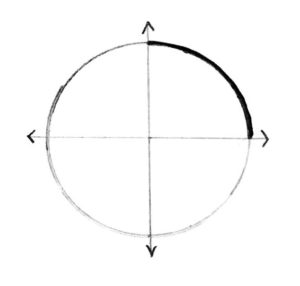 |
How about if he went only a quarter of the way around the circle. How far will he have gone?
Answer: \(\frac{\pi}{2}\) radiuses |
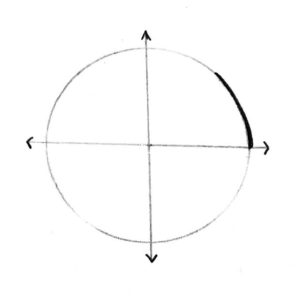 |
How about \(\frac{1}{8}\) of the way?
Answer: \(\frac{\pi}{4}\) radiuses |
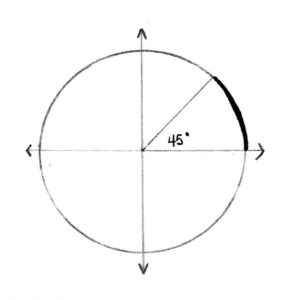 |
Is there an easier way to express the idea of “walking \(\frac{1}{8}\) of the way along the circle”?
Encourage discussion here. The student may suggest an angle measure. Draw the angle and show it is 45°. |
Let’s make a table:
| Portion of circle | degrees | radiuses |
| All the way | ||
| Halfway | ||
| \(\frac{1}{4}\) of the way | ||
| \(\frac{1}{8}\) of the way |
Have the student reason and fill in the blank cells as follows:
| Portion of circle | degrees | radiuses |
| All the way | 360° | \(2\pi\) |
| Halfway | 180° | \(\pi\) |
| \(\frac{1}{4}\) of the way | 90° | \(\frac{\pi}{2}\) |
| \(\frac{1}{8}\) of the way | 45° | \(\frac{\pi}{4}\) |
Let’s do some mental math. Don’t look at the table.
How many radiuses is 360°?
How many radiuses is 45°?
How many radiuses is 90°?
How many radiuses is 180°?
Do you like the word “radiuses”? Can you think of a better word?
In 1873, Lord Kelvin’s little brother was writing exam questions. He didn’t really like the word “radiuses” either, so he coined a new word: a radian.
Update the table and change the “radiuses” column label to “radians.”
So how many radians is it for our mouse to walk around the entire circle?
Answer: \(2\pi\) radians
How many radians are equal to 180°?
Answer: \(\pi\) radians
How many radians are equal to 90°?
Answer: \(\frac{\pi}{2}\) radians
Now suppose we wanted to track the position of the mouse as he travels around the circle. Let’s say that the circle has a radius of 1 unit. We call this the “unit circle.”
Add tick marks for x and y at 1 and -1:
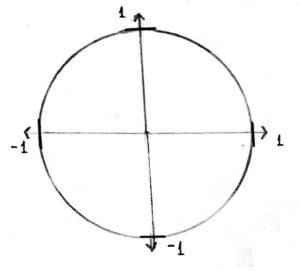
Let’s track his position using x and y coordinates:
| Portion of circle | degrees | radians | x | y |
| All the way | 360° | \(2\pi\) | ||
| Halfway | 180° | \(\pi\) | ||
| \(\frac{1}{4}\) of the way | 90° | \(\frac{\pi}{2}\) |
Have the student reason and fill in the first three rows of blank cells as follows:
| Portion of circle | degrees | radians | x | y |
| All the way | 360° | \(2\pi\) | 1 | 0 |
| Halfway | 180° | \(\pi\) | -1 | 0 |
| \(\frac{1}{4}\) of the way | 90° | \(\frac{\pi}{2}\) | 0 | 1 |
We call the x-coordinate on the unit circle “cosine” and the y-coordinate “sine.” The name sine comes from the Arabic word for bowstring. The y-value of the position of the mouse resembles half of a bowstring:
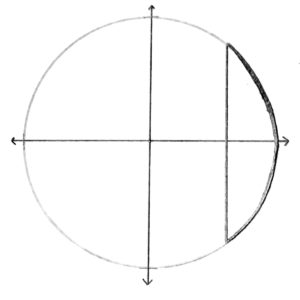
The prefix “co” in cosine means “complement.”
Update the table and change the “x” column label to “cosine” and the “y” column label to “sine”:
| Portion of circle | degrees | radians | cosine | sine |
| All the way | 360° | \(2\pi\) | 1 | 0 |
| Halfway | 180° | \(\pi\) | -1 | 0 |
| \(\frac{1}{4}\) of the way | 90° | \(\frac{\pi}{2}\) | 0 | 1 |
What is the sine of \(\frac{\pi}{2}\) radians? In other words, what is the y-coordinate of the mouse when he has gone \(\frac{\pi}{2}\) radiuses around the circle?
Answer: 1
Mental math:
What is the cosine of \(\pi\)?
Answer: -1
What is the sine of 0?
Answer: 0
What is the sine of \(\frac{3\pi}{2}\)?
Answer: -1
People tend to think of geometry and algebra are two different kinds of math. But when you get to calculus, you will see that they are very closely related. This is especially true when you use radians. There is something special about radians that makes some elements of calculus very simple and elegant. That is why most mathematicians prefer to measure angles in radians instead of degrees.