Number: A Figure and a Step Onward

Editor’s note: In October of 2017, we shared our first Parents’ Review article by Irene Stephens, entitled “Mathematics.” In the Editor’s Note, we highlighted the pivotal role played by Miss Stephens in the development of Charlotte Mason’s distinct approach to math instruction. We also shared some elements of Stephens’s life chronology, including how she ended up at Mason’s House of Education. However, our story ended in 1912, with the publication of “Mathematics” in The Parents’ Review.

Later that same year, Miss Stephens left Ambleside and went to India.^[1] Once in India, she put her gifts and training to good use and became the “head of a training department.”^[2] After fifteen years in India, she “returned to Ambleside in 1927 and joined the staff of the P.U.S., when among her responsibilities was included the whole of the work in Science and Mathematics.”^[3] She returned to find the PNEU still relying on her The Teaching of Mathematics to Young Children for guidance in math instruction, listed as late as Programme 111 (1928).

But Stephens did not pass the PNEU mantle on to some other math thinker. Instead, she wrote a slightly revised and expanded version of her 1911 paper,^[4] and called it “Number. ‘A Figure and a Step Onward.’” It was first published in the 1929 Parents’ Review in two parts (January and September), and we are proud to share both parts here for the first time on the Internet. This paper became the new resource recommend by the PNEU; in Programme 115 we read, “See also the papers by Mrs. W. Stephens in January and July [sic] numbers of the P.R.”

Soon afterwards, “Number. ‘A Figure and a Step Onward’” was published as a standalone booklet. This booklet became the recommended math resource from Programme 116^[5] up through Programme 127 (1933), the last regular programme we have in the archive. But amazingly, in the archive we do find a “Preparatory Programme” from 1961 which recommends “Number, by Mrs. I. Stephens (P.N.E.U., 1/-).” This programme gives extraordinary confirmation that Stephens’s two texts on math instruction formed the backbone of Charlotte Mason math for a half-century — from 1911 to 1961.

Of course we note something interesting in the 1961 programme: Miss I. Stephens has become Mrs. I. Stephens. It turns out that Stephens returned from India in 1927 with more than just rich experience gained on a new continent. She also came back with a new name. We are confident that Mrs. W. A. Stephens, the author of “Number. ‘A Figure and a Step Onward’” is in fact Irene Stephens. It seems most likely that she married a Mr. W. A. Stephens, and followed the convention of the day in taking on his full name in formal communication, simply prepending it with “Mrs.” But by 1961, such conventions were already old-fashioned, and so the author of Number is given as (a modern) “Mrs. I. Stephens.”^[6]

Was 1961 the end of the road for Charlotte Mason math? The method survived for 50 years. It’s been just over 50 years since that “Preparatory Programme.” In that time, persons haven’t changed; they are still persons. Absolutes haven’t changed; truth is still truth. At Charlotte Mason Poetry we believe that Irene Stephens’s ideas have a very bright future. As long as there are persons — and truth — we believe there will be room for Charlotte Mason math.

– Art

By Mrs. W. A. Stephens
The Parents’ Review, 1929, pp. 35-41, 575-585

Part I

“A figure and a step onward; not a figure and a florin” was the motto of the Pythagorean school of philosophy hemmed in and pressed upon even in their day by the crowd of those to whom a florin rather than a step onward was the only sensible end of wisdom and learning. The same crowd is still about us; the practical ends and use of learning are so much emphasised and dwelt upon that more than ever do we need to look upon the other side. We need to try and get for ourselves or give to our pupils the feeling that it is the “step onward” that counts most; the delectable land of learning is so well worth exploring for its own sake, if we find a pot of gold at the end of our journey that is good, but it is the journey and the things we have discovered along the way that count.

Miss Mason called arithmetic “Number” as being a much more comprehensive word for that subject which, under the name of arithmetic, was so apt to be thought of as only sums. She wanted the children to get a real sense of number; some vision of its innate power and beauty far beyond the sum of the moment. Arithmetic is learning about numbers; not learning to work sums. Miss Mason taught us that “Education is the science of relations” and that a child should feel from the very beginning that his relations with number are opening up to him yet another realm of beautiful and wonderful things for his enjoyment and delight.

[In Introduction to Mathematics,] Dr. Whitehead tells us that the “really profound changes in human life all have their origin in knowledge pursued for its own sake,” and quotes Lord Beaconsfield, “A practical man is a man who practises the errors of his forefathers.” The men whose discoveries have eventually revolutionised thought or advanced civilisation have been those seldom or never influenced by “practical” considerations; Menaechmus, Diophantus, Descartes, Leibnitz, Faraday, were all pre-eminently philosophers and scholars. It is matter of common knowledge now that the Egyptians measuring their muddy fields were not the real geometers; practical necessity drove them, it is true, to a crude mechanical geometry very useful for measuring or building but absolutely stopped and held up within the bounds of those simple requirements. There the great science of geometry might have remained forever were it not that the interest of the Greeks was captured. The Greek mind seized on that crude geometry of surfaces and, delighting in knowledge for its own sake, found therein a new field for mental and abstract exploration, a new direction for thought and expression. With an eager hunger for new knowledge philosopher after philosopher carried on the research until a most magnificent series of conclusions were arrived at—at the service of humanity indeed—but put there by the thinkers driven onwards by an urge to know and not to get.

One may multiply such examples as this. More than four thousand years ago the people of China understood the practical use of the magnetic compass needle, but the investigations which led to the revelation of the laws of magnetism and electricity received no help from them. Thousands of years later the magnetic compass came to Europe and then the theory behind the experience, the abstract of which the magnetic needle was a concrete expression, stimulated the thirst for knowledge of Western thinkers and theorists who again one after another explored ever deeper into the realm of that science which we now know as electro-magnetism. It is those thinkers and dreamers who have made possible our electric lights and irons, our telegraphs and telephones, not the practical Chinaman with his useful bit of magnetic iron.

A glance through any account of the story of mathematics will show the reader that mathematics was and is the beautiful servant of man; at hand to help him to solve the problems of the natural and physical world about him or to discover or invent that which shall help on the march of civilisation. By its help men may tunnel towards each other from opposite sides of a mountain and meet unerringly in its midst; the borings for the Simplon Tunnel begun twelve miles apart fitted so perfectly when the borers met in the heart of the mountain that the mistake was only three inches one way and eight inches the other. Again men may slash across a continent a line which, like the Panama Canal, shall join two oceans “opening the door to a thousand fresh sources of wealth and prosperity”: and yet hold apart the rushing together of those mighty waters by a barrier so frail that it was broken by the pressure on a button of President Wilson’s finger two thousand miles away. By the aid of mathematics engineers may build a bridge like the one across the Forth and use sixty thousand tons of steel which hold together and bear severe strain and pressure only because the most carefully calculated provision has been made for such things as expansion due to temperature, distortion due to the sun acting on one side of the structure, or the wind acting on one side of the bridge. Behind all this achievement and all the present-day annihilation of time and space stands the hand-maid mathematics; and her development and ever fuller revelation to humanity have been accomplished by those to whom the acquisition of mathematical knowledge was an end in itself worthy of the best of their lives and powers. The square root of (-1) may seem to the uninitiated so elusive and unreachable an idea that any attention paid to it would be, from the practical point of view, sheer waste of effort. The mathematician has however deemed it worthy of his thought and work and, as a result, the square root of (-1) now plays its own significant and important part in the elucidation of many a difficult “practical” calculation.

Thus in many ways mathematicians have given into our hands a power over the forces of nature which has enabled us to do great things of a practical and useful kind; but let us not forget that their inspiration was from within and not from outward circumstance. Each one of them in his turn was not bound within the limits of practical usefulness to the immediate needs of his age and time; but rather heard the call of “something’s waiting, go and find it,” and spent himself to know and still to know.

Plato defines philosophers as “those who set their affections on that which in each case really exists,” and again as, “those who are able to grasp the eternal and incommutable.” How fully and exactly does mathematics fulfil both these qualifications; no truth exists more really than a mathematical truth, no truth can so fitly be called eternal, nor reach by so many paths the incommutable. It is fitting then to hear the same teacher say “Pursued in the spirit of a philosopher and not of a shopkeeper arithmetic has a very great and elevating effect.” When the sum of the world’s learning had not reached its present total but was, in comparison, a very minute quantity arithmetic had not lost its rainbow sheen; wise men stood rapt in awe before the golden gate-way to enchanted ground which arithmetic represented. The most learned and wisest were full of wonder at what seemed like the “magic” of numbers which might, they felt, unravel the deepest mysteries of their lives. With the course of time and the accumulation of knowledge upon knowledge we have perhaps allowed ourselves a rather blasé attitude towards numbers: thrills which require no effort of thought are cheap and numerous and the modern developments of science so exciting that few if any of us spare time to be surprised at the simple things: such as for instance, why should 6 be 1+2+3 or 1x2x3 while 5 or 7 are never anything but 5×1 or 7×1? And this attitude creeps into our work; arithmetic becomes the “dull” subject, a matter of obvious common-place and tiresome necessity. When a little child comes to the gate-way of number he comes as did the sages of old ready and hoping to be led into a magic land, to exercise his faculty of wonder once more in his so wonderful world, and alas, how often he is disappointed! He is shown, in effect, not a Delectable Country but a Slough of Despond with nothing beyond it but further Sloughs of Despond through which he must plough for years on weary years. We can only help him by getting back ourselves to the philosophical approach to mathematics, back to the place where we regain our own wonder and sense of reverence and awe before those things which the science and art of number can reveal to us.

A modern professor recently wrote of mathematics as the “controller of destinies, source of delight, fount of emotion, breeder of romance.” Astronomy is full of romantic stories of discovery and fulfilment made possible by mathematics, and we may read of and in imagination share in the soul-stirring joy of some of the earlier observers. There were those for instance, in the middle nineteenth century, who dared to say that the dread portent shown in the “Year of the Stars,” 902 A.D., when the heavens rained fire upon the city of a dying Moorish King, was but a manifestation of the same phenomenon as had been displayed in great magnificence to two explorers in South America in 1799 and that, moreover, would be shown again upon the earth on the night of the 13^th of November, 1866.

The world held its breath in suspense before such daring, but behold upon the exact night it came: that wonderful exhibition of celestial fireworks now called the Leonids.

To predict mathematically on paper and find one’s prediction fulfilled in the sky is now almost a commonplace of astronomical research and still further wonders reward our reading. We find for one thing that the Pole Star consists of four stars though no telescope yet invented has ever shown more than two of them; and that in the celestial universe there are myriads upon myriads of such stars. They are entirely beyond the utmost reach of perception by physical sense; no telescope has ever shown the faintest glimmer of one of them; and yet, thanks to mathematical law, thousands of them are tabulated in a catalogue! The chemical composition of each one, the size and shape of its path in the sky, and the length of time it takes to complete this mighty orbit; these things are written down almost as though those stars were objects in a museum. Before wonders such as these surely even the least mathematical among us must feel his spirit stirred.

How sad that this subject, ethereal as faëry and powerful beyond telling, should find no other adjective than “useful” to justify us in imparting it to our children. Number to the philosophers of old was a touchstone of learning; it was worthy of their greatest respect and deepest thought. Let us take from them this gift with the others they have given us; this thought of Number as worthy of our best, æsthetically satisfying as an art, beckoning onward as a science, and luring us ever forward towards increasingly enchanting prospects ahead.

It may be argued that this attitude towards mathematics, or the appreciation of some of its fascination and beauty, is a gift only given to the very few: but we venture to think that such an argument is more a habit of thought than a proven truth. In days not long past we were accustomed to think that music was a heaven-sent gift to a chosen few and a hard exercise in discipline and the sterner virtues to those not of this blessed minority. In this present-day we are told that every child can be a musician of some degree; that, given the right beginning, every child can be taught to think musically, to improvise for himself, and to appreciate intelligently the music of others. Though the world may never produce another Beethoven, the teachers of music are learning how to put their pupils into the right relationship with this subject, so that it is a gift to every one of them of opportunity for happy and joyful experiences; not, as it has been for the majorities of the past, a grinding between the millstones of drudgery and despair.

It seems that the same is true of the teaching of Number, it all depends on the teacher’s attitude and the right beginning, that we ourselves have been led the wrong way and found only an arid desert is no reason for imposing that way upon our pupils. We may not nurture an Isaac Newton in our classes, but we can if we get the right outlook and take the right way with the children, send forth a set of people whose relation with the Science of Number is a happy and inspiring one, whose exercise of the art of Number is a source of satisfaction, whose whole attitude towards the subject is a desire to know more for the joy of knowing it. When a pupil says: “What is the use of working this sum?” the teacher may be sure that she has taken the wrong way somehow, that she has failed to keep in sight for herself the witchery and fascination of her subject and so both her pupil and herself are in danger of falling soon into that Slough of Despond from which it is so hard to escape. Let us try to capture for ourselves something of the lure of this realm of Number, to see if but dimly a vision of its beauty and feel the appeal of its romance, then we need not fear but that the children will go with us and Number come into its own.

Let us then assume that we have now come to the place where we feel that we must not limit ourselves to the aim of teaching mathematics to a child simply in order that when he is a man he may conduct his daily business correctly; this may follow as a result of mathematical training but is not its raison d’ être. We have ceased to consider mathematics only in its most practical manifestations or to think of it as an unpleasant necessity in the day’s routine; we have felt for ourselves a little of its glamour and illumination. We see how it brings to the learner both mental food and æsthetic satisfaction, together with a craving for still further knowledge of its kind, and we are therefore ready to put down very exactly its value to the character and mind of the individual.

We may say that any era of the world’s civilisation may be judged largely by the state of its mathematics and we therefore assume that the value of the acquisition of some amount of mathematical training is undisputed even by those unable to realise it in exact terms of intellectual training and power.

[In Home Education,] Miss Mason says, “Of all his early studies perhaps none is more important to the child as a means of education than that of arithmetic. The chief value of arithmetic like that of the higher mathematics lies in the training it affords to the reasoning powers and in the habits of insight, readiness, accuracy, intellectual truthfulness it engenders.” “Let his arithmetic lesson be to the child a daily exercise in clear thinking and rapid careful execution, and his mental growth will be as obvious as the sprouting of seedlings in the spring.”

The cultivation of the habits of clear thought, of insight and accurate judgment, of reasoning ability and the rapid grasp of a situation, of a general alertness and readiness of the mind to respond to stimulus, come with mathematical training and are some of the terms in which we express its results. To the student it will be within himself a source of inspiration and refreshment and an outlet for the expression of his power.

It may perhaps be well to end this introduction to the teaching of arithmetic with a hint of warning. “The laws of number are the decrees of God,” and as such inexhaustible in wonder and complexity, but they are not all of His decrees, they are only a part of His plan and not the whole of it. We must give Number its rightful place in the scheme of the universe while at the same time we guard ourselves from being drawn into the crazy by-paths which have attracted humanity through all the ages. These have led men into mazes of bewilderment from which they try to emerge by attempts to prove that “all life is number,” or that humanity and divinity can be reduced to a system of curves and equations.

Number is but one of the many beautiful patterns which go to make up the complete fabric of fulness of living which is a gift from God. Our relations with Number take their place with our relations with History and Literature, Art and Science, as revelations of the Supreme Power working in and through all human life and manifesting itself in these many ways.

Part II

The first part of this paper was meant, in some degree, to indicate the spirit and feeling with which we might approach the teaching of Number to small children so as in no way to provide, by our teaching, any hindrance to the happiest relations between our pupils and their subject. The following pages will give a few suggestions for the theory and the actual practice of this teaching. Those who have made some study of the subject will have formulated theories of their own, or will be able to use, with discrimination and selection, some of the many books which are now available. There still remain some however, parents and teachers, who have not time or opportunity to formulate schemes or pass books in review and yet must teach small children from day to day: to them it is hoped that the lines of work indicated herein may be welcome. Some useful and valuable suggestions have been found in Miss Punnett’s Groundwork of Arithmetic, and Dr. Ballard’s Teaching the Essentials of Arithmetic. Both of these writers have a wide and varied experience in the teaching of Mathematics, and we are grateful for the benefit of their conclusions.

Theory

For the earliest Number lessons the first broad general principles to be kept in mind are these: (1) That a Number lesson must be short and concentrated, very bright and quickly over; (2) That the lessons must be given first with concrete objects familiar to the child’s environment and as varied as possible and then must pass gradually to work with pure number; (3) That everything used in the lessons must be large and clear and unconfusing.

To enlarge somewhat upon these points:—

(1) All number processes, however simple, are processes of logical reasoning and require the fullest attention of the mind during the process. They require also quick thought, one that leaps from step to step, dawdling and laggard thinking mean only stumbling and confusion. Such intense mental activity cannot be exercised for long periods at a stretch, and a short, fully-utilised, number time is the ideal generating ground for those mathematical habits which are going to be so useful to our pupils all their lives. We must never, too, lose sight of the fact that all the simple mathematical processes we are teaching our young pupils are one day going to be their instinctive habits in a much more complicated and difficult mathematical experience: these must therefore be habits that will help and not hinder.

(2) “The beginning of Arithmetic is counting”—we count in order to know, and the answer is a number. “How many” is the new idea we are bringing into the child’s field of consciousness; and we want to present it as relating to the everyday world. Number is not a special thing living only in a box with certain buttons, or beads, or counters, it belongs to everything. When we want to do really exciting things with numbers,—and it would be quite inconvenient to move tables and chairs, or root up trees, or catch birds or fish to work with,—we, for convenience sake, use our counters or beads to represent the trees or birds.

Children of five-and-a-half or six will, as a matter of fact, come to school with some idea of counting, but in the first lessons it is well to fix the quality of “number” to everything possible, the children themselves, their legs, arms, eyes, ears, the objects in the room, trees in the garden, doors and windows, cars and animals out-of-doors. Then, for convenience only, we resort to things easily handled, such as sticks or counters, and these must be as varied as possible, both for the sake of keeping the pupil’s interest, and because we must not nail our numbers down to one particular kind of object. The idea of number must bring with it a suggestion of everything and not merely of the same old box of sticks or beads, or of only the fingers of our hands and the toes of our feet.

As time goes on the convenient concrete objects can be replaced by strokes made on a piece of paper; and finally we leave even these behind and work with pure number and a mental picture only of the subjects of our “sums.”

(3) This is necessary from two points of view: (a) The reading of figures is a great strain on the eyes of young children, and the counting over or handling of slippery minute objects such as small beads or beans is a strain, not only on their eyes, but on their hands and nerves as well, and tends to a distracting of attention and a confusion of mind; (b) Easily handled objects of fair size, and clear large figures which can be distinguished at a glance, mean that the pupil’s mind and attention are not confused but can be concentrated on the main arithmetical thought. The utmost clarity of thought is the chief essential to a number lesson, therefore all outward circumstances which may help this are desirable, and all those which may cause confusion are to be avoided.

The Curriculum

It is impossible to lay down rigid rules about the amount of ground to be covered in a given time because each child must work at this subject individually and at his own pace, provided that he does work, but experience suggests that, as a minimum, it is reasonable in the first year to expect that a child will learn to work with the numbers 1 to 12 learning:—

(1) That each number is one of a series with more numbers stretching away in front of it and other numbers extending behind it. Each number has its place in the line and will always be greater than the ones behind it and less than the ones before, and can be made by adding another number to any of the former, or taking another number away from one of the latter. This idea is conveyed by counting, which is the very first thing to be learnt. Counting is the ultimate and fundamental basis of all arithmetical processes and nothing can be done without it.

(2) That each number has its individual value and represents a group of a certain size which can be broken into smaller groups or made by joining together smaller groups. Thus 7 potatoes or 7 dogs can be made into smaller groups of 4 potatoes and 3 potatoes, 4 dogs and 3 dogs, or can be formed by combining 5 potatoes and 2 potatoes, 5 dogs and 2 dogs.

(3) That a number also conveys an idea of part of a continuous quantity, or a relation of a greater to a lesser quantity, and it is this use we make of number when we weigh or measure things. Underlying it again is, of course, our root base counting, but to count the milk in a can, or tea in a tin, or the length of a room, we must take first a quantity of milk or tea, or a length of wood, to represent one and count how many of those we have.

It is to help us in introducing this idea of number that we carry our lessons on to 12 without stopping at 10 as a natural stage. We get the 12 inches in a foot, 12 months in a year, and 12 pennies in a shilling, with which it is quite easy to work, and which quite naturally convey the idea of this aspect of numbers. Miss Punnett in her book also recommends 12 as a stopping place in preference to 10.

(4) The processes of addition and of simple subtraction.

(5) The signs +, =, -, and x.

(6) To write, and to recognise when written, the symbols for the numbers 1 to 12, taking 10, 11, 12 simply as symbols without any significance yet. It is enough at the beginning that as a general rule children should write only the answers to their sums, but they must of course learn to write each figure as they come to it. It is very easy in the early stages to confuse 2, 3, 5, 8, and therefore only very clear plain figures without ornament should be used, and care taken to emphasise the salient characteristic of each, such as a straight stroke and good bar to the top of 5, two open halves to 3, and firmly closed ones to 8.

(7) The “twice times” table up to 2×6=12.

In order to achieve the foregoing our lessons will have to include some on counting, some on the combinations of groups to form numbers, on individual numbers, on measuring and simple money, on the meaning and use of the signs, and the writing of the symbols.

The need of careful work with these earlier numbers cannot be over emphasised, they form the groundwork of all later Arithmetic, and all the more difficult processes are but extensions of the simpler. If the numbers 1 to 12 can be manipulated easily and quickly, and their relations to each other are known, the bigger numbers will follow without difficulty and will not need to be worked in the same detail. It is at this early stage too that a child becomes accustomed to the connection between the abstract and the concrete and, to a certain degree, between both these and the written symbol. These numbers, if used with thought and ingenuity, provide enough variety and interest to ensure that no lesson need be a dull one.

Arithmetic for children of six to seven in the Parents’ Union School goes beyond the course of work mentioned above. The work set for children in Form Ib would suppose them, at the end of their first year, to be able to work with figures up to 99 and to (1) Add three numbers in a column with carrying of tens; (2) Subtract numbers such as 27 from 40; (3) Know the tables up to 6×12 and do sums using the same; (4) Do simple division, dividing numbers less than 100 by numbers up to 6; (5) Work sums in the addition and subtraction of pounds, shillings and pence with farthings expressed as 1/2d. or 1/4d.; (6) Understand the meaning of yard, inch, pound, square, oblong, half, quarter. This is not in any way a rigid arrangement, as Miss Mason distinctly says that there can be no gaps in an Arithmetic course and that a child must work straight on at his own pace. Since very many children however do attain the above standard by the time they are seven some of the practical teaching necessary to it will be discussed later on in this paper. The suggestions made have in view small classes such as are found in home schoolrooms and private schools.

Practice

For help and convenience the teacher should have at hand collections of easily handled sticks, beads of two large sizes and varied colours, large beans and pebbles, reversible counters or draughtsmen, and cards. These cards would consist of some with one of the numbers printed clearly on each, others with a combination of numbers clearly written, e.g., 6+2=, 7-4=, etc., and others again containing several of the combinations that make one number collected on the one card, e.g.,

3+4=

7-3=

7-4=

5+2=

7-2=

2+5=

7-5=

would designed to teach the composition of the number 7 as made up of 3 and 4 or 5 and 2. These are useful when the child has to be left to work alone while the teacher attends to something else. A large chart with clearly printed numbers 1 to 12 would also be useful.

The First Lesson

This would include for bright children numbers up to and including 5; for dull ones, numbers only up to 3; and would deal with the recognition of each of these as a group by itself, the simple combinations that make it, and the writing of the symbols 1 and 2. It would proceed somewhat as follows:—

(1) The introduction would tell that we are now going to learn about numbers which tell us how many of anything. Whenever we want to know how many there are of something there is a number ready to help us, and give the answer.

(2) Teacher would now ask how many there were of various things in the room or easily visible. How many arms has John? How many legs? How many legs has the table? How many pencils are there on the desk? How many trees out of the window? How many panes in the window? doors in the room? The questions should be confined to small numbers up to 5, and if it is noticed that the children have to count 1, 2, 3, 4,…before giving their answers they should be encouraged to do without this and to give just the answer straight away, i.e., to recognise at a glance a group of 1, 2, 3, 4, or 5, things, the amount possible varying with the brightness of the children.

(3) The teacher would now ask a few carefully graded questions such as: How many noses have 2 boys? how many eyes? How many tails have 3 dogs, 4 cats? If Mary had 4 Easter eggs and someone gave her another, how many would she have? How many if she were given 4 more? If Tom had 5 eggs and broke 3, how many would he have left?

It may be found necessary in some cases to let sticks or pebbles represent the objects in the sum, and to obtain the result by working with these, but these very simple number combinations would most probably be already known to most children; if the teacher finds that one particular combination is not known to one particular child she should make sure that that child gets practice in it by varying examples. A number of these small examples should be looked out and prepared beforehand if there is likely to be any loss of time in thinking of them.

(4) The symbols 1 and 2:—As we are going to use these numbers and make friends with them we should like to know them when we see them. When we see Michael’s face and body coming along we say, “Here’s Michael,” and in the same way it would be nice to be able to say, “Here’s a 2, or a 3, or a 4.” 1 is the easiest number to recognise, just a straight stroke, and everyone can draw it easily. Let the children draw a few 1’s standing up as straight and beautiful as possible.

2 is more difficult, but goes like this: the teacher will make a very plain 2 on the board, large and made only of a hook and a horizontal bar. The children will practise making 2’s with crayon and small boards, or pencils and paper.

The Second Lesson

To give further practice in very simple number combinations and to introduce the symbol 3. The teacher should have ready her large number chart and each child should have a few sticks and a few beads.

(1) Begin with simple questions on number combinations, not stopping at 5 but going on to 7 or 8, and using the ideas of addition and subtraction, e.g., We picked 3 apples off one tree and 4 off another, how many had we? Mary’s mother baked 6 little cakes and Mary ate 2, how many were left? The examples must be taken from the child’s immediate sphere of interest and, if necessary, a little visual or concrete help given, e.g., the teacher may draw a rough quick picture of the 6 cakes and rub out 2; or the children may use their beads, counting out 6 and removing 2, and trying to give the answer 4 without actually counting if possible.

(2) The symbol 3: See that the children remember 1 and 2 by pointing to them on the chart and asking for their names, or ask the children to show them on the chart, or to say what they look like. Then show the picture of a large 3. The symbol for 3 is a little apt to be confused with a 2 in the beginning, it is therefore just as well to emphasise the difference. In making a 2 we go round a corner thus 2, then along a little way 2, and stop: when we want to get on to 3 we come round the second corner too, thus 3.

The children might now each write a few 3’s on their boards, looking at the one on the blackboard, or getting the 3 by beginning with a 2 and turning it into a 3, the former is preferable.

(3) The teacher will now put up her number chart again and take a little quick drill in the symbols 1, 2, 3: (a) The teacher points in turn to any one of the three symbols on the chart and the class holds up the correct number of fingers; (b) The teacher points as above and the class puts out on the desk the right number of sticks, always making a tidy row or pattern, not just a heap; (c) Repeat (b), using beads.

(4) The class to write a row of 3’s on individual boards or in books.

The Third Lesson

To give further practice in counting up to 7 or 8, recognition of groups up to 5, combination of groups to make numbers up to 7 or 8, and writing 2 or 3. Class will need boxes of pebbles, marbles, etc.

(1) The class to count up to 7 or 8, to hold up 4 fingers, 6 fingers, 3 fingers, 5 fingers, etc., as required.

(2) The teacher to ask the class to bring her in turn, without counting, 4 books, 3 marbles, 5 sticks, 3 slates, 1 pencil box, 5 pebbles, 2 flowers, etc., etc. If there is difficulty about getting 4 and 5 without counting a child may be allowed to consider 4 as 3 and then 1, 5 as 3 and then 2.

(3) Small examples to be done orally, e.g.: (a) A man has 2 pieces of wood and he wants 6, how many more must he have?; (b) How many are 2 and then 3 and then 1?; (c) A house had 5 chimneys and the wind blew down 2, how many were left?; (d) There were 7 ducks on a pond and 4 dived down, how many were left? Then 2 came up again, how many were there now?

(4) The teacher to dictate 1, 2, and 3 in any order and let the children write them, teacher rubbing out quickly any mistake made so that a wrong visual impression may not remain.

The Fourth Lesson

To introduce the symbol 4 and work easy problems, using strokes on paper instead of concrete objects. Each child to have four cards printed with the symbols 1, 2, 3, 4, one on each card.

(1) Let the class point out or make collections of 4 things in the immediate vicinity, e.g., buttons on someone’s frock, pots on the window sill, legs of chairs or tables, legs of two children together, panels in the door.

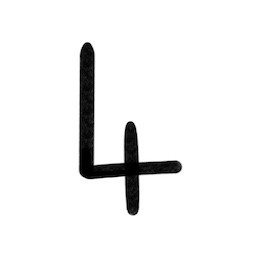(2) We want to know what 4 looks like when we see him, he looks like an L with a nail through the bottom bar. Draw a 4 on the board, let children find it on the chart, let everybody draw a 4.

(3) Let each child set out his cards in a row in front of him. Teacher will now give some easy problems with answers not greater than 4, and the children in turn will give the answer orally and will then pick out and show the card which bears that answer.

Let each child have his board or a piece of paper handy, and if there is difficulty about a problem show how we can pretend that strokes on the paper are the things in the sum and cross some out, or add some more, as the sum demands.

Examples of suitable problems: (a) One little girl has 2 pockets on her jersey and another little girl has only 1. How many pockets?; (b) There were 5 pictures in a room and 2 had no frames, how many had frames?; (c) A little boy planted 7 bulbs and 4 came up, how many did not?; (d) There were 8 branches on a tree and 4 were chopped down, how many were left? 2 more were chopped down, how many left now?; (e) A little boy went for a walk with 6 marbles in a bag and 5 dropped through a hole in the bag, how many did he bring home? His mother gave him 3 more, how many did he have now?; (f) A little girl’s uncle gave her 8 pennies and she bought a book for 6 pence and sweets with the rest, how many pennies did she spend on sweets?; (g) A boy had a motor bus with 6 wheels and 3 came off, how many did the bus have left?; (h) A caterpillar ate the leaves off 1 twig on Monday, off another twig on Tuesday, and off 2 twigs on Wednesday, of how many twigs did he eat the leaves?

The Fifth Lesson

To introduce the symbol for 5 and to continue the practice in simple problems, and in recognising the symbols up to 5.

It is not necessary to set out the steps of this lesson as the preceding ones will give an idea of how it should proceed. To ensure that the symbols are correctly recognised the following device is useful:—Give each pupil a number of cards bearing the figures 1, 2, 3, 4, 5, singly, the cards to be all mixed together, also a number of beads in two colours. Let the pupil set out a card on his desk or board and beside it make a pattern using the right number of beads, e.g., if the card is a 4 he might put out 4 beads in a row or in a square. The child thus fixes the idea of a connection between the symbol and the group for which it stands, the patterns in two colours give him a little scope for making his larger group out of two smaller ones, e.g., 1 blue and 3 yellow beads the first time, and 2 blue and 2 yellow the second time, a 4 appears on his card.

As an alternative to the above the teacher might write upon the board the figures 1 to 5 far apart and in any order and with some repetition. The children would then be asked to arrange upon their desks a pattern of beads to represent each figure in the order in which it is written upon the board.

All the above lessons are tentative and are meant as suggestions rather than rigid models. Some children will probably find them too easy, others too hard, and they must be adapted accordingly. Every child can realise a group of 3 things, and most children can realise a group of 5 with practice, so that the first 5 numbers can well be taught together. After the symbol for 5 has been learnt it is convenient to teach the signs +, =, and soon after – and x. Again, it is well to take a lesson on each of the numbers 6 to 12 individually as it comes, some teachers advocate that these might be given in any order, e.g., a lesson on 10 before one on 8, but as children themselves always prefer things done in just the right way, and as clearness and order matter so much in this subject, it would seem better to take the numbers in their proper sequence and to take a lesson on 6 before we give one on 7.

The Sixth Lesson

To introduce the signs + and =.

(1) Ask a very simple question such as “There were 2 lambs in a field and 1 more jumped in, how many were there now?” How do we know that there were 3? Because 2 and 1 make 3. Suppose we want to write this, we know how to write a 2 and a 1 and a 3, and there is a nice short way of writing “and” as well as “make.” Instead of “and” we write + and instead of “make” we write =. So we put down 2+1=3, which means 2 and 1 make 3.

(2) The children would now be asked to read from the board various combinations of numbers up to 5, 1+4=5, 2+2=4, 1+3=4, 2+3=5, etc., saying “and” and “make” for + and =.

(3) The children would now be allowed to write some of these sums themselves, the teacher asking very simple questions such as “If I picked 2 roses off one bush and 2 off another, how many had I?” and the children writing 2+2=4.

(4) Using the combinations written on the board the teacher would ask the children to show her with actual things how 4 and 1 made 5, 2 and 2 made 4, etc. They could do this with reversible counters, with small and large sticks, or with things in the room.

The Seventh Lesson

On the number 6. To introduce the symbol for six, the numbers which added make 6, the idea of two 3’s being 6. Each child to have 6 pennies and a sixpence. The teacher must also have ready several small familiar articles with which to play at “Shop.”

(1) Show the symbol 6 and allow it to remain in evidence throughout the lesson.

(2) Let the children count 6 of anything they can see, 6 fingers, 6 children, and so on, quite quickly and shortly, and then count and set out the 6 pennies in a row.

(3) Divide the row of 6 pennies, putting 1 aside to the right, how many on the left? 5, because 5 and 1 make 6. As we have learnt how to write this we can put down on the board 5+1=6. Now put 2 pennies away to the right, and we have 4+2=6, putting 3 aside in the same way we have 3+3=6, and we notice that there is an equal number on each side so that 6 is made of two 3’s. Now we go on and get in the same way

2+4=6

1+5=6

Now we have finally written on the board the whole table of numbers which added make 6, allow this to remain on the board.

(4) Ask questions on the table: (a) Peter had 6 chocolates and gave away 4, how many had he for himself?; (b) If he had made the 6 chocolates into 2 equal shares, how many would there have been in each?; (c) In a room there were 2 tables and each had 3 legs, how many legs?; (d) A bird had 6 eggs in its nest and 1 got broken, how many left?; (e) John had only 1 book, but on his birthday he got 5 more, how many did that make?; (f) Mary was 6 years old and her little sister was only 3, how many years older was Mary?; (g) How many legs have a little boy and his dog?

(5) Pennies are used to buy things and we will play at buying but, as the pennies are so heavy, we have a neat little silver coin which counts just the same as 6 pennies and is called sixpence. Pile the 6 pennies together and put a sixpence beside each pile, remember they count the same. Each child will now come with its sixpence and buy something, telling the teacher how many pennies it wants in change.

(6) If there is time some of the children can be shopkeeper in turn and give the right change without being told, the purchaser to notice if it is right.

Note: The formatting of the above article was optimized for online viewing. To access a version which is formatted more similarly to the original, and which includes the original page numbers, please click here.

Footnotes for the Editor’s Note

^[1] “In the May number of the Parents’ Review came the sad news of the retirement of Mrs. Stephens, Principal of the P.U.S. It was in 1909 that she first came to Scale How to help Miss Kitching in her secretarial work for Miss Mason and to lecture to the students on Mathematics, Astronomy and Physics. In 1912 she left to go to India, but returned to Ambleside in 1927 and joined the staff of the P.U.S., when among her responsibilities was included the whole of the work in Science and Mathematics. In 1948 she was appointed Principal.” From “Annual Report,” by Elizabeth Molyneux, in The Parents’ Review, volume 63 (1952), p. 190.

^[2] “Mrs. Stephens brings experience as a lecturer and head of a training department in India, besides twenty-one years in the work and administration of the P.U.S.” From “Report on the Parents’ Union School,” in The Parents’ Review, volume 59 (1948), p. 485. The “twenty-one years” clearly refer to the period from 1927 to 1948.

^[3] Molyneux, op. cit., p. 190.

^[4] “Mrs. Stephens has re-written her pamphlet on the subject of Arithmetic, prepared some years ago at the request of the Board of Education. It now forms the Introduction to a complete scheme of Arithmetic which has been started for all Forms of the P.U.S., including Form V. and work for the Cambridge School Certificate.” From “Books,” in The Parents’ Review, volume 41 (1930), p. 521.

^[5] Form 1 for Jan.-Mar. 1930 includes this line: “Beginners: Number, by Mrs. W. A. Stephens (P.N.E.U. Office, 4d.).”

^[6] The “Preparatory Programme” from 1961 says, “Number, by Mrs. I. Stephens (P.N.E.U., 1/-).” By comparison, A list of “P.N.E.U. publications” in the 1959 Parents’ Review (volume 70) includes this line: “Number: ‘A Figure and a Step Onward’. By Mrs. W. A. Stephens. 6d” (p. 29). These clearly refer to the same resource; Mrs. I. Stephens and Mrs. W. A. Stephens must be the same person. The 1958 Parents’ Review (volume 69) also includes a reference to “Mrs. Irene Stephens, formerly Principal, Parents’ Union School” (p. 14).

Subscribe: Apple Podcasts | Spotify | Amazon Music